We study two kinds of generalized random Fibonacci sequences defined by F1=a, F2=b and one of the following induction formulas:
linear case: for n>0, Fn+2 =
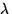 Fn+1
Fn+1 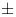 Fn
Fn non-linear case: n>0, Fn+2 = |
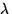 Fn+1
Fn+1 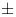 Fn|
Fn| where
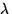 is of the form
is of the form 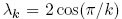 for some k
for some k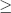 3, and each
3, and each 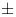 sign is independent and either + with probability p or - with probability 1-p (0 < p
sign is independent and either + with probability p or - with probability 1-p (0 < p 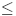 1). For k=3,
1). For k=3, 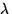 =1 and we recover random Fibonacci sequences.
=1 and we recover random Fibonacci sequences. Our main result is that the exponential growth of Fn for 0 < p
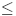 1 in the linear case, and for 1/k
1 in the linear case, and for 1/k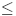 p
p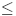 1 in the non-linear case, is almost surely given by
1 in the non-linear case, is almost surely given by 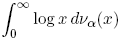
where
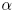 is an explicit function of p depending on the case we consider, taking values in [0, 1]k-1, and
is an explicit function of p depending on the case we consider, taking values in [0, 1]k-1, and 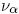 is an explicit probability distribution on R+ defined inductively on generalized Stern-Brocot intervals.
is an explicit probability distribution on R+ defined inductively on generalized Stern-Brocot intervals. Our method relies on some reduction process and makes use of Rosen continued fraction expansion. In the linear case, it gives an explicit form for Furstenberg's invariant measure. It is easier in the non-linear case to which the standard theory does not apply.